11th grade

Here is a short breif explanation of matrices

A Matrix is an array of numbers:

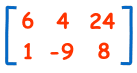
A Matrix
(This one has 2 Rows and 3 Columns)

We talk about one matrix, or several matrices.

There are many things we can do with them ...

Adding

To add two matrices: add the numbers in the matching positions:

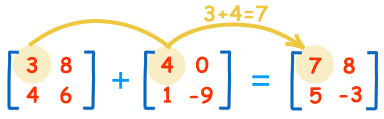
These are the calculations:

3+4=7	8+0=8
4+1=5	6-9=-3

The two matrices must be the same size, i.e. the rows must match in size, and the columns must match in size.

Example: a matrix with 3 rows and 5 columns can be added to another matrix of 3 rows and 5 columns.

But it could not be added to a matrix with 3 rows and 4 columns (the columns don't match in size)

Negative

The negative of a matrix is also simple:

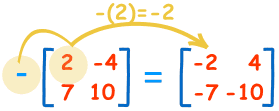
These are the calculations:

-(2)=-2	-(-4)=+4
-(7)=-7	-(10)=-10

Subtracting

To subtract two matrices: subtract the numbers in the matching positions:

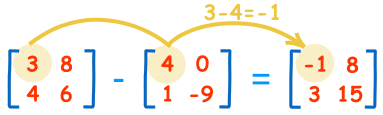
These are the calculations:

3-4=-1	8-0=8
4-1=3	6-(-9)=15

Note: subtracting is actually defined as the addition of a negative matrix: A + (-B)

Multiply by a Constant

We can multiply a matrix by some value:

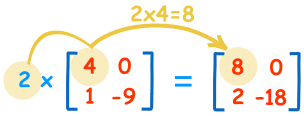
These are the calculations:

2×4=8	2×0=0
2×1=2	2×-9=-18

We call the constant a scalar, so officially this is called "scalar multiplication".

Multiplying by Another Matrix

But to multiply a matrix by another matrix we need to do the "dot product" of rows and columns ... what does that mean? Let us see with an example:

To work out the answer for the 1st row and 1st column:

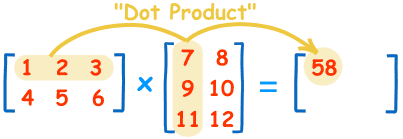
The "Dot Product" is where we multiply matching members, then sum up:

(1, 2, 3) • (7, 9, 11) = 1×7 + 2×9 + 3×11 = 58

We match the 1st members (1 and 7), multiply them, likewise for the 2nd members (2 and 9) and the 3rd members (3 and 11), and finally sum them up.

Want to see another example? Here it is for the 1st row and 2nd column:

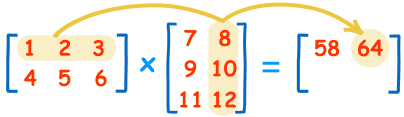
(1, 2, 3) • (8, 10, 12) = 1×8 + 2×10 + 3×12 = 64

We can do the same thing for the 2nd row and 1st column:

(4, 5, 6) • (7, 9, 11) = 4×7 + 5×9 + 6×11 = 139

And for the 2nd row and 2nd column:

(4, 5, 6) • (8, 10, 12) = 4×8 + 5×10 + 6×12 = 154

And we get:

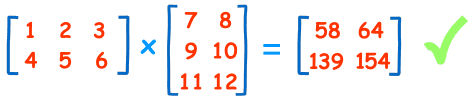
DONE!

Dividing

And what about division? Well we don't actually divide matrices, we do it this way:

A/B = A × (1/B) = A × B^-1

where B^-1 means the "inverse" of B.

So we don't divide, instead we multiply by an inverse.

And there are special ways to find the Inverse ...

Transposing

To "transpose" a matrix, swap the rows and columns. We put a "T" in the top right-hand corner to mean transpose:

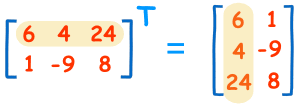
Notation

A matrix is usually shown by a capital letter (such as A, or B)

Each entry (or "element") is shown by a lower case letter with a "subscript" of row,column:

Rows and Columns So which is the row and which is the column? Rows go left-right Columns go up-down To remember that rows come before columns use the word "arc": ar,c

Example:

B =

Here are some sample entries:

b_1,1 = 6 (the entry at row 1, column 1 is 6)

b_1,3 = 24 (the entry at row 1, column 3 is 24)

b_2,3 = 8 (the entry at row 2, column 3 is 8)