11th grade

Here is a short breif explanation of matrices

A Matrix is an array of numbers:

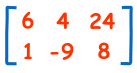
A Matrix
(This one has 2 Rows and 3 Columns)

We talk about one matrix, or several matrices.

There are many things we can do with them ...

Adding

To add two matrices: add the numbers in the matching positions:

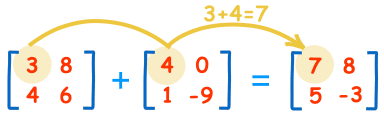
These are the calculations:

3+4=7	8+0=8
4+1=5	6-9=-3

The two matrices must be the same size, i.e. the rows must match in size, and the columns must match in size.

Example: a matrix with 3 rows and 5 columns can be added to another matrix of 3 rows and 5 columns.

But it could not be added to a matrix with 3 rows and 4 columns (the columns don't match in size)

Negative

The negative of a matrix is also simple:

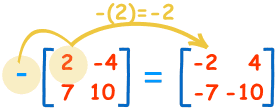
These are the calculations:

-(2)=-2	-(-4)=+4
-(7)=-7	-(10)=-10

Subtracting

To subtract two matrices: subtract the numbers in the matching positions:

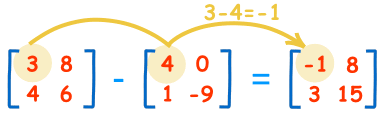
These are the calculations:

3-4=-1	8-0=8
4-1=3	6-(-9)=15

Note: subtracting is actually defined as the addition of a negative matrix: A + (-B)

Multiply by a Constant

We can multiply a matrix by some value:

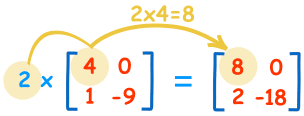
These are the calculations:

2×4=8	2×0=0
2×1=2	2×-9=-18

We call the constant a scalar, so officially this is called "scalar multiplication".

Multiplying by Another Matrix

But to multiply a matrix by another matrix we need to do the "dot product" of rows and columns ... what does that mean? Let us see with an example:

To work out the answer for the 1st row and 1st column:

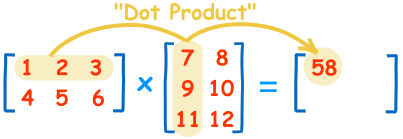
The "Dot Product" is where we multiply matching members, then sum up:

(1, 2, 3) • (7, 9, 11) = 1×7 + 2×9 + 3×11 = 58

We match the 1st members (1 and 7), multiply them, likewise for the 2nd members (2 and 9) and the 3rd members (3 and 11), and finally sum them up.

Want to see another example? Here it is for the 1st row and 2nd column:

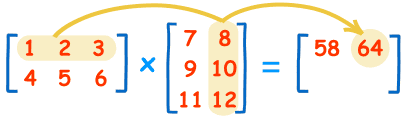
(1, 2, 3) • (8, 10, 12) = 1×8 + 2×10 + 3×12 = 64

We can do the same thing for the 2nd row and 1st column:

(4, 5, 6) • (7, 9, 11) = 4×7 + 5×9 + 6×11 = 139

And for the 2nd row and 2nd column:

(4, 5, 6) • (8, 10, 12) = 4×8 + 5×10 + 6×12 = 154

And we get:

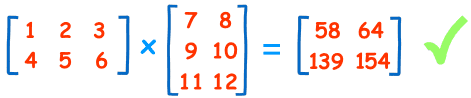
DONE!

Dividing

And what about division? Well we don't actually divide matrices, we do it this way:

A/B = A × (1/B) = A × B^-1

where B^-1 means the "inverse" of B.

So we don't divide, instead we multiply by an inverse.

And there are special ways to find the Inverse ...

Transposing

To "transpose" a matrix, swap the rows and columns. We put a "T" in the top right-hand corner to mean transpose:

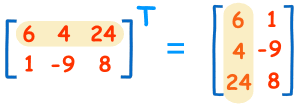
Notation

A matrix is usually shown by a capital letter (such as A, or B)

Each entry (or "element") is shown by a lower case letter with a "subscript" of row,column:

Rows and Columns So which is the row and which is the column? Rows go left-right Columns go up-down To remember that rows come before columns use the word "arc": ar,c

Example:

B =

Here are some sample entries:

b_1,1 = 6 (the entry at row 1, column 1 is 6)

b_1,3 = 24 (the entry at row 1, column 3 is 24)

b_2,3 = 8 (the entry at row 2, column 3 is 8)

7th grade

This  is the rule used for all adding integers or fractions or rational numbers 

Subtracting with unlike signs 

Subtract  like signs

I will futher explain this on Monday 

Week 2

Hey you guys hope you are enjoying your weekend  the following below is basically the schedule for next week.

7th grade:

On Monday we will do a breif discussion on adding and subtracting rational numbers and then go to multiplying integers. Wednesday we will do dividing integers

8th grade

On Tuesday we will finish fraction sense and on Thursday we will go on to the next chapter 

11th grade

Tuesday  we will start Matrices

Please remember to bring your report card grades and the short answer on why you join my club.please and thank you. God bless😊😊

7th grade:What page are guys at in your math books.

7th Grade 

Since you guys said that yall haven't done multiplying and dividing integers, I found something that is simple and that yall will understand. Hope it helps!!!